Principal Component Analysis (PCA) is a powerful and well-established data transformation method that can be used for data visualization, dimensionality reduction, and possibly improved performance with supervised learning tasks. In this use case blog, we examine a dataset consisting of measurements of benign and malignant tumors which are computed from digital images of a fine needle aspirate of breast mass tissue. Specifically, these 30 variables describe specific characteristics of the cell nuclei present in the images, such as texture symmetry and radius.
Data Exploration
The first step in applying PCA to this process was to see if we can more easily visualize separation between the malignant and benign classes in two dimensions. To do this, we first divide our dataset into train and test sets and perform the PCA using only the training data. Although this step can be considered feature engineering, it is important to conduct the train-test split prior to performing PCA because the transformation takes into account variability in the whole dataset and would lead to information in the testing set leaking into the training data otherwise.

The resulting PCA resource lists the top Principal Components (PC), sorted by their Percent Variation Explained. In this example, we can see that PC1 accounts for 45.12% of the total variance in the dataset, and the top 7 PCs alone account for approximately 90% of the Percent Variation Explained. We can further explore which of the original fields are contributing the most to the various PCs by inspecting the bar chart provided on the left. The three greatest contributors to PC1 turn out to be “concave points mean”, “concavity mean”, and “concave points worst”. Based on this information, we can begin to conclude that features related to concavity are highly variable and possibly discriminative.

A PCA transformation yields new variables which are linear combinations of the original fields. The major advantages of this transformation are that the new fields are not correlated with one another and that each successive Principal Component seeks to maximize the remaining variance in the dataset under the constraint of being orthogonal to the other components. By maximizing variance and decorrelating the features, PCA-created variables can often perform better in supervised learning – especially with model types that have higher levels of bias. However, this is performed at the expense of overall interpretability. Although we can always inspect the contributions of our original variables on the PCA fields, a linear combination of 30 variables will always be less straightforward than simply inspecting the original variable.
Data Visualization

After plotting the dataset according to only the top 2 Principal Components (PC1 and PC2) and coloring each data point by diagnosis (benign or malignant), we already can see a considerable separation between the classes. What makes this result impressive is that we used no knowledge of our target variable when creating or selecting for these Principal Component fields. We simply created fields that explained the most variance in the dataset, and they also turned out to have enormous discriminatory power.
Predictive Modeling
Finally, we can evaluate how well our Principal Components fields work as the inputs to a logistic regression classifier. For our evaluation, we trained a logistic regression model with identical hyperparameters (L2 regularization, c=1.0, bias term included) using 4 different sets of variables:
- All 30 original variables
- All Principal Components
- Top 7 PCs (90% PVE)
- Top 2 PCs only
The results are visualized in the Receiver Operating Characteristic (ROC) curve below, with a malignant diagnosis serving as the positive class and sorted by Area Under the Curve (AUC). In general, all of the models in this example performed very well, with rather subtle differences in performance. However, the scale of the input data varied widely. Most notably, a model using only two variables (PC1 and PC2) performed with an AUC of >0.97, and very close to the top performing model with AUC >0.99.
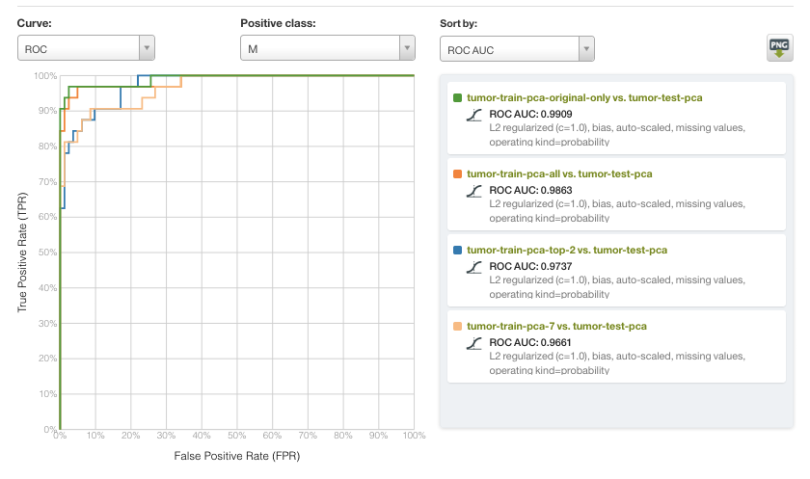
As part of Occam’s Razor of Machine Learning, it is often advantageous to utilize a simpler model whenever possible. PCA-based dimensionality reduction is one method that enables models to be built with far fewer features while maintaining most of the relevant informational content. As such, we invite you to explore the new PCA feature with your own datasets, both for exploratory visualization tasks and as a preprocessing step.
Want to know more about PCA?
If you would like to learn more about Principal Component Analysis and see it in action on the BigML platform, please reserve your spot for our upcoming release webinar on Thursday, December 20, 2018. Attendance is FREE of charge, but space is limited so register soon!

