The venerable K-means algorithm is the a well-known and popular approach to clustering. It does, of course, have some drawbacks. The most obvious one being the need to choose a pre-determined number of clusters (the ‘k’). So BigML has now released a new feature for automatically choosing ‘k’ based on Hamerly and Elkan’s G-means algorithm.
The G-means algorithm takes a hierarchical approach to detecting the number of clusters. It repeatedly tests whether the data in the neighborhood of a cluster centroid looks Gaussian, and if not it splits the cluster. A strength of G-means is that it deals well with non-spherical data (stretched out clusters). We’ll walk through a short example using a 2 dimensional dataset with two clusters, each has a unique covariance (stretched in different directions).
G-means starts with a single cluster. The cluster’s centroid will be the same as you’d get if you ran K-means with k=1.

G-means then tests the quality of that cluster by first finding the points in its neighborhood (nearest to the centroid). Since we only have one cluster right now, that’s everything. Using those points it runs K-means with k=2 and finds two candidate clusters. It then creates a vector between those two candidates. G-means considers this vector to be the most important for clustering the neighborhood. It projects all the points in the neighborhood onto that vector.

Finally, G-means uses the Anderson-Darling test to determine whether the projected points have a Gaussian distribution. If they do the original cluster is kept and the two candidates are rejected. Otherwise the candidates replace the original. In our example the distribution is clearly bimodal and fails the test, so we throw away the original and adopt the two candidate clusters.
After G-means decides whether to replace each cluster with its candidates, it runs the K-means update step over the new set of clusters until their positions converge. In our example, we now have two clusters and two neighborhoods (the orange points and the blue points). We repeat the previous process of finding candidates for each neighborhood, making a vector, projecting the points, and testing for a Gaussian distribution.
This time, however, the distributions for both clusters look fairly Gaussian.
When all clusters appear to be Gaussian, no new clusters are added and G-means is done.
The original G-means has a single parameter which determines how strict the Anderson-Darling test is when determining whether a distribution is Gaussian or not. In BigML this is the critical value parameter. We allow ranges from 1 to 20. The smaller the critical value the more strict the test which generally means more clusters.
Our version of G-means has a few changes from the original as we built on top of our existing K-means implementation. The alterations include a sampling/gradient-descent technique called mini-batch k-means to more efficiently handle large datasets. We also reused a technique called K-means|| to quickly pick quality initial points when selecting the candidate clusters for each neighborhood.
BigML’s version of G-means also alters the stopping criteria. In addition to stopping when all clusters pass the Anderson-Darling test, we stop if there are multiple iterations of new clusters introduced without any improvement in the cluster quality. The intent is to prevent situations where G-means struggles on datasets without clearly differentiated clusters. This can results in many low utility clusters. This part of our algorithm is tentative, however, and likely to change. We also plan to offer a ‘classic’ mode that stops only when all clusters pass the Anderson-Darling test.
All that said, we’ve been happy with how well G-means handles datasets with complicated underlying structure. We hope you’ll find it useful too!




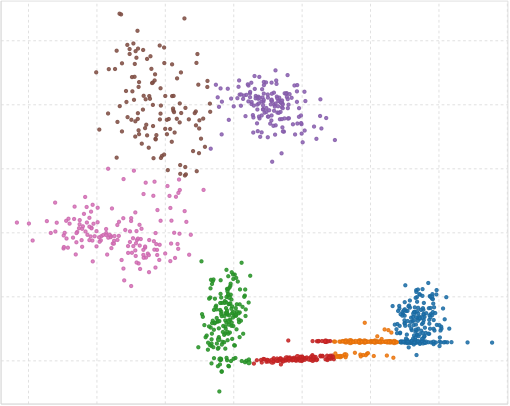
I’m trying to implement G-means. How is the vector that connects the centroids of two K-means clusters computed? Will component-wise vector subtraction do? What about the sign/direction of the vector, that is, which vector is subtracted from which?